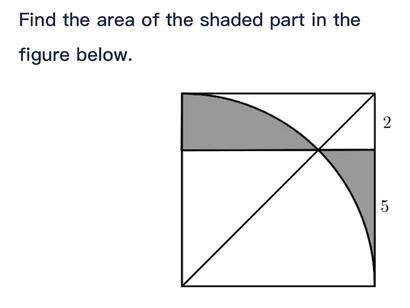
在某些几何题目中,图形的对称性可能会误导我们的直觉判断。比如不久前 @delphij 发的一道辅导其五年级女儿的数学题。
错误解法及分析
很多人在看到这道题时,会将两块阴影部分之一,沿正方形的对角线对称镜像,补全另一部分为一个长方形,长为 5,宽为 2。面积为 \(2 \times 5 = 10\)。但这种解法是错误的。注意到图中的四分之一圆弧、正方形对角线、边长按 2:5 分割的平行线,这三者看起来像是交于同一点,但实际上并不相交。它们只是位置接近。做题者很容易被误导。
正确解法
作为小学生,如果直接把这道题当成一道错题忽略,也未尝不可。不过,我们是具有大学同等学力的知识人,发扬爱折腾的精神。下面讨论一下若要满足上述三线交于一点的假设,此题能不能做出来。
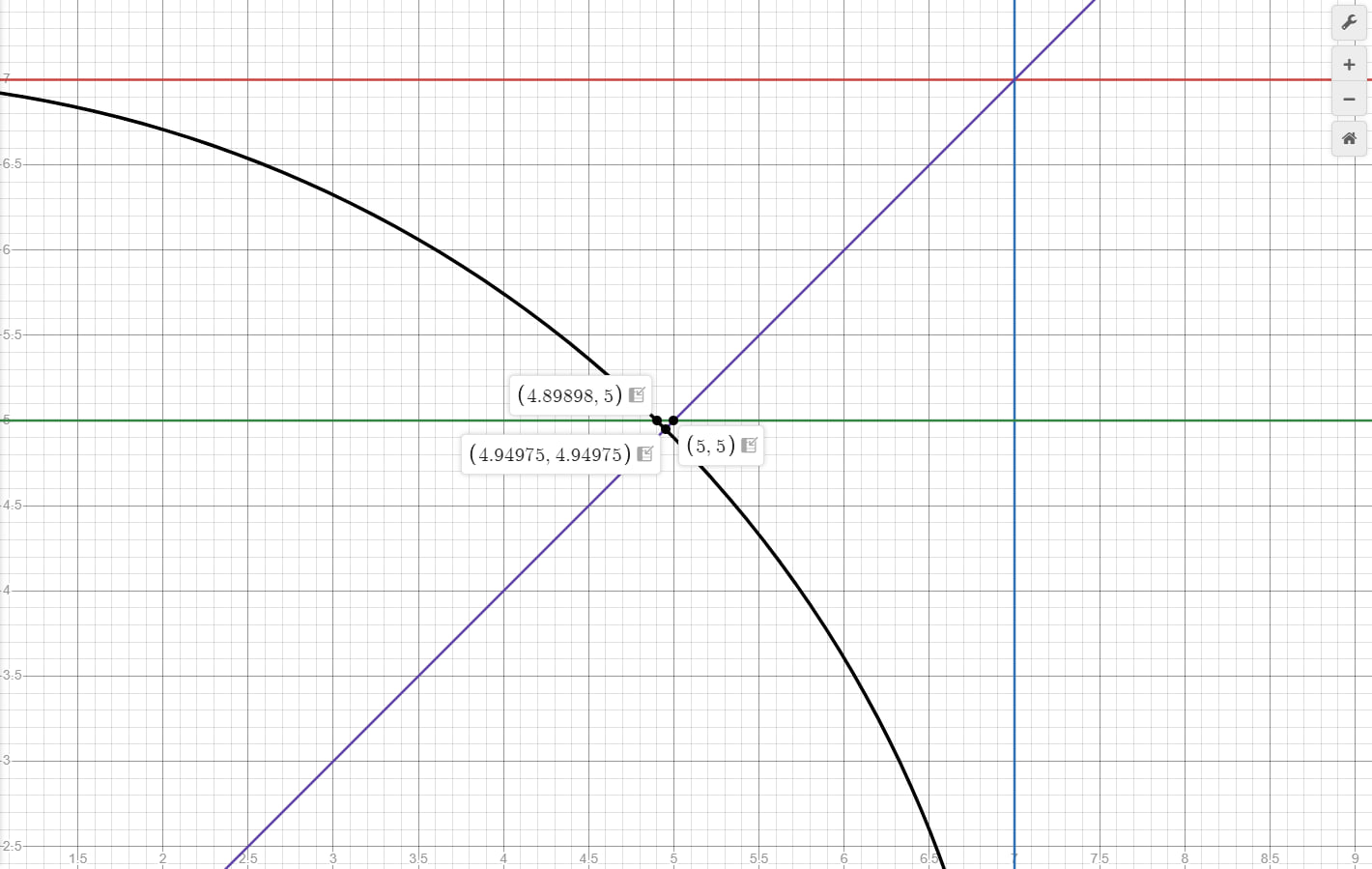
显然,必须放弃中间那条线“与边长平行”的假设。可以在 GeoGebra 上简单绘图。
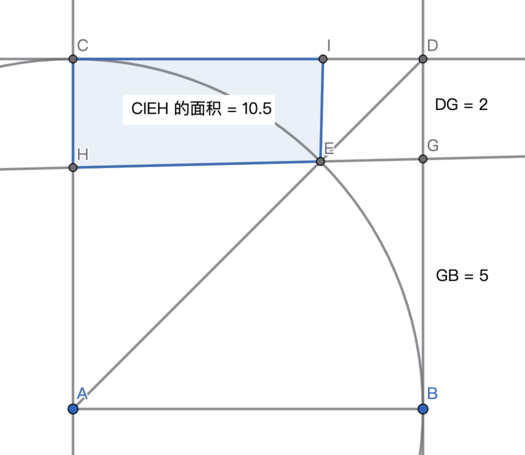
取点 G 关于 AD 的对称点 I。根据对称性,我们要计算的阴影区域面积,即为四边形 CIEH 的面积。GeoGebra 给出的这部分面积是 10.5。
那么,10.5 是精确值还是估算值呢?我希望进一步求出精确解。
解析解法
最终我们需要计算的阴影区域面积,即为四边形 CIEH 的面积。下面我们把四个点的坐标一一算出来。
设正方形边长为 7,其四个顶点分别为:
$$ A = (0, 0) $$ $$ B = (7, 0) $$ $$ C = (0, 7) $$ $$ D = (7, 7) $$
根据原题图,G 点的坐标为:
$$ G = (7, 5) $$
圆弧与对角线 AC(即 x = y)交于点 E,满足:
$$ x^2 + y ^2 = 49 $$ $$ x = y $$
求得该方程组在第一象限内的解,得到:
$$ E = \left( \frac{7}{2} \sqrt{2}, \frac{7}{2} \sqrt{2} \right) \approx (4.9497, 4.9497) $$
延长 EG 线段,与纵轴(x=0)交于点 H,可求得:
$$ H = \left( 0, 2 \sqrt{2} + 2 \right) \approx (0, 4.8284) $$
取点 G 关于 AD 的对称点 I:
$$ I = (5, 7) $$
这下 C、I、E、H 四点的坐标就都有了。
通过 Shoelace 公式计算面积
可以用 Shoelace 公式来计算平面内任意多边形中间围成的面积。就 CIEH 四边形而言
正向乘积 S₁:
$$ \begin{aligned} S_1 &= x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁ \\ &= 0 × 7 + 5 \cdot \left(\frac{7}{2}\sqrt{2} \right) + \left(\frac{7}{2}\sqrt{2}\right) \cdot \left( 2\sqrt{2} + 2\right) + 0 × 7 \\ &= \frac{35}{2}\sqrt{2} + 14 + 7\sqrt{2} \\ &= \frac{49}{2}\sqrt{2} + 14 \end{aligned} $$
反向乘积 S₂:
$$ \begin{aligned} S_2 &= x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄ \\ &= 5×7 + \frac{7}{2}\sqrt{2}×7 + 0 + 0 \\ &= 35 + \frac{49}{2}\sqrt{2} \end{aligned} $$
面积:
$$ \begin{aligned} S &= \frac{1}{2} \left| S_1 - S_2 \right| \\ &= \frac{1}{2} \left| 14 + \frac{49}{2}\sqrt{2} - 35 - \frac{49}{2}\sqrt{2} \right| \\ &= \frac{1}{2} \left| -21 \right| \\ &= 10.5 \end{aligned} $$
确认了 10.5 为精确结果,并非近似值。
通过拆分三角形计算面积
不用 Shoelace 公式也可以用初等方法计算四边形 CIEH 面积。
可将其拆为两个三角形:△CIE 和 △CEH
- △CIE:底边为 CI,E 到该边的垂直距离为高;
- △CEH:底边为 CH,E 到该边的水平距离为高。
△CIE
- 底 \( = 5 \)
- 高 \( = 7 - \frac{7}{2}\sqrt{2} \)
- 面积:
$$ \begin{aligned} A_1 &= \frac{1}{2} \cdot 5 \cdot \left( 7 - \frac{7}{2}\sqrt{2} \right) \\ &= \frac{35}{2} - \frac{35}{4} \sqrt{2} \end{aligned} $$
△CEH
- 底 \( = 7 - (2\sqrt{2} + 2) \)
- 高 \( = \frac{7}{2}\sqrt{2} \)
- 面积:
$$ \begin{aligned} A_2 &= \frac{1}{2} \cdot \left( 7 - (2\sqrt{2} + 2) \right) \cdot \frac{7}{2}\sqrt{2} \\ &= \frac{1}{2} \cdot \left( 5 - 2\sqrt{2} \right) \cdot \frac{7}{2}\sqrt{2} \\ &= \frac{35}{4} \sqrt{2} - 7 \end{aligned} $$
合并后总面积为:
$$ \begin{aligned} A &= A_1 + A_2 \\ &= \left(\frac{35}{2} - \frac{35}{4} \sqrt{2} \right) + \left(\frac{35}{4} \sqrt{2} - 7\right) \\ &= 10.5 \end{aligned} $$
结果与 Shoelace 公式计算的相同。
comments powered by Disqus